1.
i
Укажите номер выражения, которое определяет, сколько сантиметров в х м 9 дм.
| 1) 100х + 9; | 2) 100х + 90 | 3) 90x | 4) 10x + 90 | 5) 10x + 9 |
1) 1
2) 2
3) 3
4) 4
5) 5
РЕШУ ЦТ — математика ЦЭ
Вариант № 181
см, а 9 дм — это 90 см.2.
i
Если число а расположено на координатной прямой левее числа b, то зависимость между числами а и b можно записать в виде неравенства:
1) a > b
2) a ≥ b
3) a < b
4) a ≤ b
5) a = b
3.
i
Если 15% некоторого числа равны 33, то 20% этого числа равны:
1) 44
2) 46
3) 55
4) 56
5) 66
где x — неизвестное число.
4.
i
Если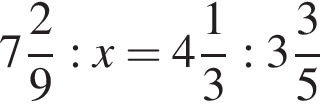 
— верная пропорция, то число x равно:
1) 
2) 
3) 
4) 
5) 
5.
i
Пусть x1 и x2 — корни уравнения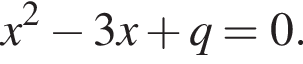 
Найдите число q, при котором выполняется равенство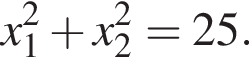 
1) -8
2) -3
3) 8
4) 4
5) -5
а 
Зная то, что 
6.
i
Для неравенства (8 − x)(x + 3) ≥ 0 укажите номера верных утверждений.
1) Число 0 не является решением неравенства;
2) неравенство равносильно неравенству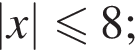 
3) количество всех целых решений неравенства равно 12;
4) неравенство верно при x ∈ [−2; 3];
5) решением неравенства является промежуток [−8; 3].
1) 2, 4
2) 3, 5
3) 3, 4
4) 1, 2
5) 1, 5
Таким образом, верные утверждения указаны под номерами 3 и 4.7.
i
Найдите сумму целых решений неравенства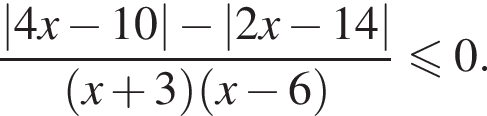 
совпадает со знаком разности 
имеем:
корни знаменателя 
Поэтому: 
Целые решения — числа −2, 4, 5. Их сумма равна 7.8.
i
Решите неравенство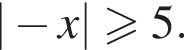 
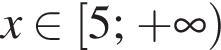
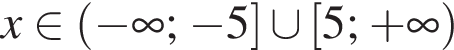
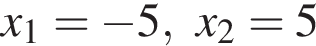
1) 
2) 
3) 
4) 
5) 
9.
i
Выразите x из равенства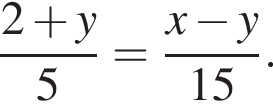 
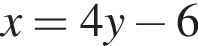
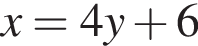
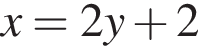
1) 
2) 
3) 
4) 
5) 
10.
i
Решите уравнение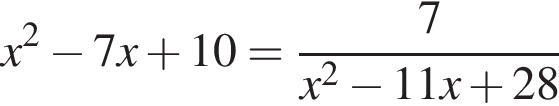 
и найдите сумму его корней.
Получим:
найдем по теореме Виета, она равна 9.
равносильно уравнению 
искать ОДЗ не требуется.11.
i
Пусть (x1; y1), (x2; y2) — решения системы уравнений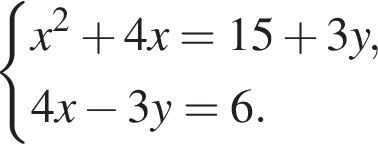 
Найдите значение выражения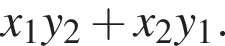 
12.
i
Найдите сумму целых решений неравенства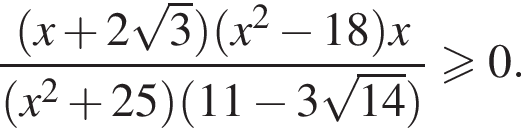 
поскольку 
Число, 
Домножим неравенство на эти числа, поменяв знак, и решим его.
Целыми решениями неравенства являются числа −4, 0, 1, 2, 3, 4, их сумма равна 6.13.
i
Найдите произведение наименьшего целого решения на количество всех натуральных решений системы неравенств
14.
i
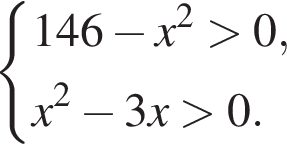
Определите координату точки А, изображенной на координатной прямой.
1) −7;
2) −1;
3) 
4) −8;
5) 
15.
i
Результат упрощения выражения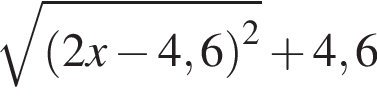 
при −1 < x < 1 имеет вид:
1) 9,2 − 2x
2) −2x − 9
3) 2x + 9,2
4) 2x
5) −2x
16.
i
Упростите выражение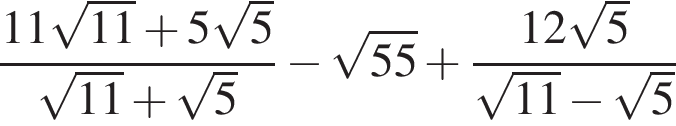 
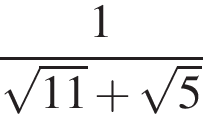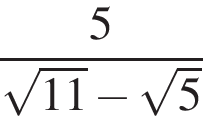1) 
;
;2) 
;
;3) 
;
;4) 
;
;5) 
.
.
17.
i
Найдите произведение всех корней (корень, если он единственный) уравнения
18.
i
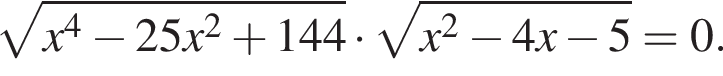
Упростите выражение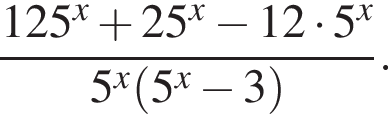 
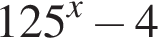
1) 
2) 
3) 
4) 
5) 
тогда дробь примет вид: 
Тем самым, исходное выражение равно 
19.
i
Значение выражения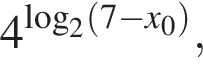 
где x0 — корень уравнения 
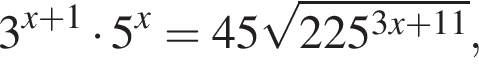равно ... .
Получаем:
20.
i
Найдите сумму целых решений неравенства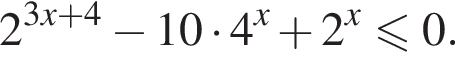 
тогда получим:
Их сумма равна −6.21.
i
Вычислите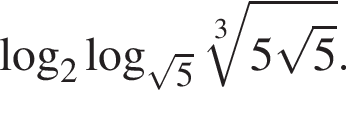 
1) −1
2) 0
3) 0,5
4) 1
5) 2
22.
i
Найдите значение выражения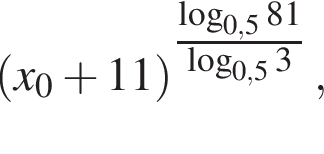 
где x0 — корень уравнения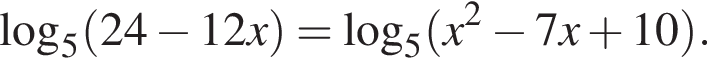 
23.
i
Найдите произведение всех целых решений неравенства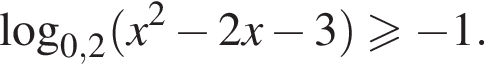 
24.
i
Упростите выражение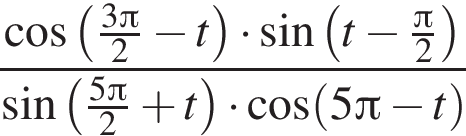 
1) 
2) 
3) 
4) 
5) 
25.
i
Найдите значение выражения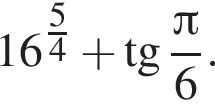 
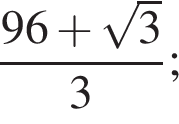
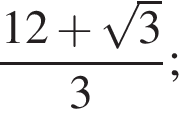
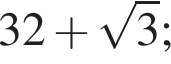
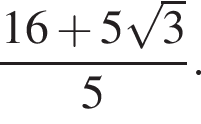
1) 
2) 
3) 
4) 
5) 
26.
i
Найдите сумму корней уравнения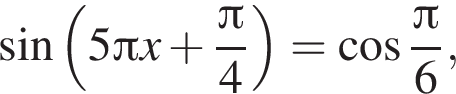 
принадлежащих промежутку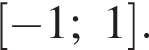 
1) 0
2) 0,1
3) 0,4
4) 0,5
5) 2,1
27.
i
Укажите номера уравнений, которые являются равносильными:
1. 
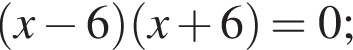
2. 
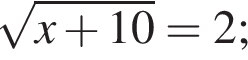
3. 
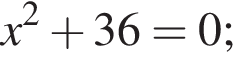
4. 
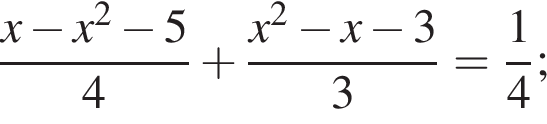
5. 
1) 1, 2
2) 2, 4
3) 3, 4
4) 1, 5
5) 3, 5
— корней нет;
28.
i
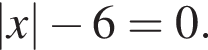
Найдите сумму всех целых решений неравенства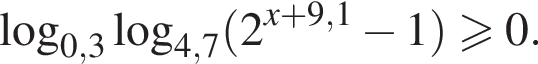 
29.
i
Арифметическая прогрессия (an) задана формулой n-го члена an = 5n − 2. Найдите разность этой прогрессии.
1) 3
2) −7
3) 5
4) 7
5) −5
где d — разность арифметической прогрессии. Коэффициент перед n и есть разность арифметической прогрессии, он равен 5.30.
i
Из пунктов A и B, расстояние между которыми 160 км, одновременно навстречу друг другу выехали два автомобиля с постоянными и неравными скоростями: из пункта A — со скоростью a км/ч, из пункта B — со скоростью b км/ч. Через некоторое время автомобили встретились. Составьте выражение, определяющее расстояние (в километрах) от пункта A до места встречи автомобилей.
1) 
2) 
3) 
4) 
5) 
Тогда время, прошедшее с начала движения до момента встречи — 
Из пункта A ехал автомобилист со скоростью a, поэтому расстояние от пункта A до места встречи автомобилей равно 
31.
i
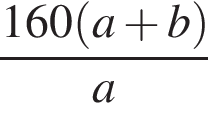
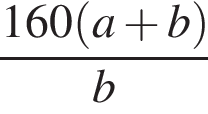
Двое рабочих выполняют некоторую работу. Сначала первый работал 
часть времени, за которое второй выполняет всю работу. Затем второй работал часть времени, за которое первый закончил бы оставшуюся работу. Оба они выполнили только 
всей работы. Сколько часов потребуется рабочему с меньшей производительностью для выполнения этой работы, если известно, что при совместной работе они сделают ее за 3 ч 36 мин?
а второго — 
Первый рабочий работал 
время, которое он затратил, равно 
Второй работал 
Если оба они выполнили 
Пусть 
Тогда: 
Зная, что 
и 
получаем, что x = 6, y = 9, или x = 9, y = 6. Таким образом, рабочему с меньшей производительностью потребуется 9 часов.32.
i
Функция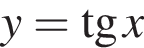 
не определена в точке:
1) 
2) 
3) 
4) 
5) 
не определена, когда 
т. е. при 
где 
Таким образом, она не определена в точке 
33.
i
Среди предложенный уравнений укажите номер уравнения, графиком которого является парабола, изображенная на рисунке:
1) 
2) 
3) 
4) 
5) 
34.
i
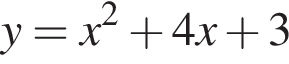
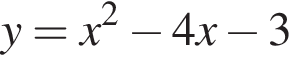
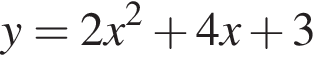
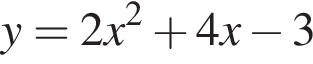
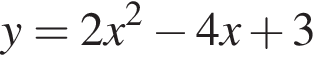
На круговой диаграмме представлена информация о продаже 200 кг овощей в течение дня. Для начала каждого из предложений А — В подберите его окончание 1 — 6 так, чтобы получилось верное утверждение.
Начало предложения
А) Масса (в килограммах) проданной капусты равна ...
Б) Отношение, выраженное в процентах, которое показывает, на сколько масса проданного картофеля меньше массы проданных помидоров, равно ...
В) Отношение, выраженное в процентах, которое показывает, на сколько масса проданной свеклы больше массы проданного лука, равно ...
Окончание предложения
1) 25
2) 40
3) 4
4) 125
5) 38
6) 19
Ответ запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например: А1Б1В4.
35.
i
Укажите номер рисунка, на котором изображены фигуры, симметричные относительно прямой l.
1) 1
2) 2
3) 3
4) 4
5) 5
36.
i
Выберите все верные утверждения, являющиеся свойствами нечетной функции 
определённой на 
и заданной формулой 
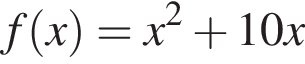при 
1. Функция имеет три нуля.
2. Функция убывает на промежутке [6; 9].
3. Максимум функции равен 25.
4. Минимальное значение функции равно -25.
5. 
6. Функция принимает отрицательные значения при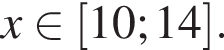 
7. График функции симметричен относительно оси абсцисс.
Ответ запишите в виде последовательности цифр в порядке возрастания. Например: 123.
при 
затем отразим построенную часть относительно оси Oy. Получим график функции 
Утверждение 2 верно.
значит, ее минимальное значение не может быть равно −25.
Утверждение 5 верно.
функция равна нулю, а значит, принимает отрицательные значения не во всех точках отрезка 
Утверждение 6 неверно.37.
i
На координатной прямой отмечены точки А, В, С, D, E. Если расстояние между A и С равно 
то ближе других к точке с координатой 0,5 расположена точка:
1) A
2) B
3) C
4) D
5) E
Поэтому необходимо отсчитать от нуля 3,5 деления — ближе всего к точке с координатой 0,5 расположена точка A.38.
i
Функция y = f(x) задана на множестве действительных чисел и является убывающей на области определения. Среди ее значений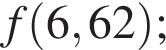 
укажите наибольшее.
1) 
2) 
3) 
4) 
5)
39.
i
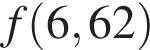
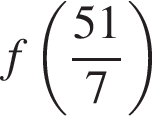
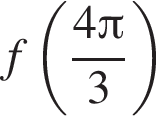
Для покраски стен общей площадью 175 м2 планируется закупка краски. Объем и стоимость банок с краской приведены в таблице.
| Объем банки (в литрах) | Стоимость банки с краской (в рублях) |
|---|---|
| 2,5 | 75 000 |
| 10 | 270 000 |
Какую минимальную сумму (в рублях) потратят на покупку необходимого количества краски, если ее расход составляет 0,2 л/м2?
л краски. Можно купить 3 банки по 10 литров и 2 банки по 2,5 литра, тогда минимальная сумма составит: 
40.
i
В основании пирамиды лежит прямоугольный треугольник, длина гипотенузы которого равна 6, острый угол равен 30°. Каждая боковая грань пирамиды наклонена к плоскости основания под углом, равным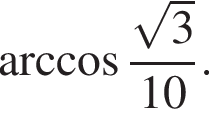 
Найдите площадь боковой поверхности пирамиды.
Тогда площадь основания равна 
